Modelling Future Climate Change

In summary, projections of future climate require projections of future forcing from GHGs, aerosols, and land-use change, which in turn depend on projections of future population and energy consumption. CO₂ is the largest contributor to human-induced climate forcing, and so CO₂ emissions and the extent to which they grow or decline will largely determine future climate.

Earth system models are based on a mathematical representation of the behaviour of the atmosphere, ocean, land surface, and cryosphere. They simulate a virtual planet using powerful supercomputers, allowing scientists to probe the connections between various physical and biogeochemical processes, e.g., how the ocean takes up heat and carbon, stores and then redistributes it. Two main ways such models are used are (1) to compare simulations with and without historical forcings to determine human versus natural forcing effects, and (2) to simulate future climate in response to various forcing scenarios.

Earth system models have some features in common with global weather-prediction models (used to make daily weather forecasts) but do not depend on the use of observations as inputs and typically operate at somewhat lower spatial resolution (i.e., the level of spatial detail is often limited to features with scales of a hundred kilometres or larger). The lower resolution is necessitated by the computing demand of the long simulations that are required. Simulations begin with the historical period (from 1850 to present), driven by observationally based climate forcing (e.g., historical changes in GHG concentrations), and then continue into the future, using different forcing scenarios (such as those described in the previous section) out to year 2100 or further (Figure 3.2).

Earth system models represent an evolution from earlier physical climate models (representing the coupled atmosphere, ocean, land, and sea ice components of the climate system) to models that go beyond this with explicit representation of the carbon cycle (Flato, 2011¹³; Flato et al., 2013¹⁴). Including carbon and other biogeochemical cycles in the models allows simulation of global interactions among ecosystems, carbon, and climate, as well as several terrestrial processes that occur at high latitudes. Changes to snow and sea ice can cause positive (amplifying) snow/ice albedo feedbacks in the climate system (Euskirchen et al., 2016¹²; Kashiwase et al., 2017²⁶; see Chapter 2, Box 2.4). As temperatures increase, the spatial extent of snow and sea ice declines, reducing the reflectivity of land and oceans, allowing more solar radiation to be absorbed, and hence further increasing temperatures. This feedback makes an important contribution to the higher rate of warming in the Arctic region, called Arctic amplification (FAQ 3.1; see Section 3.3.3). The models can also simulate increased growth of vegetation at northern high latitudes in response to a warming climate, an effect that may reduce the land surface albedo and affect the exchange of energy and water between the land and the atmosphere (Forkel et al., 2016¹⁵). Changes in permafrost in response to changing climate — leading to changes in hydrological conditions and CH₄ release (Schuur et al., 2008⁴⁴) — are also now included in some models.

How do we know that models are accurately projecting future climate? One method of measuring whether models can realistically represent the complex interconnections among climate processes is to gauge their ability to reproduce past changes. Simulations using observationally based historical forcing from 1850 onward provide the opportunity to directly compare model results to observations. The IPCC Assessment Reports have traditionally included a chapter devoted to this type of model evaluation (e.g., Flato et al., 2013¹⁴), and these provide a synthesis of the large number of scientific papers on model performance. Figure 3.5 provides one example of model evaluation, comparing the annual global mean surface air temperature from several different sources with simulations from 36 different models that participated in the fifth phase of the Coupled Model Intercomparison Project (CMIP5; see Box 3.1). As the figure shows, Earth system models are able to reproduce the observed long-term increase in temperature (heavy black lines), along with the sporadic cooling that follows large explosive volcanic eruptions. The magnitude of natural year-to-year variability is also well simulated (thin lines), although one does not expect individual ups and downs to coincide (as each model simulates its own internal variability). The heavy red line in the figure shows the multi-model average, which is an approximation of the response of the climate system to external forcing (changing GHG concentrations and aerosol amount, land-use change, variations in solar irradiance, and volcanic aerosol), upon which internal variability is superimposed. The difference between observed temperature and the multi-model average from roughly 2000 onward has been extensively analyzed (e.g., Fyfe et al., 2016¹⁷) and is due to a combination of small errors in the observational record, decadal timescale internal variability, and incomplete early 21st century volcanic forcing in the models (see Chapter 2, Section 2.3.3).

Confidence in climate model projections arises from many sources. First, climate models are solidly based on physical laws and scientific understanding of physical processes. Second, climate model results are evaluated in detail by comparing model output to observations, as described in Section 3.3.1. The model evaluation chapter in the most recent IPCC Assessment report provides many examples (Flato et al., 2013¹⁴). Third, some of the models used to make climate projections are also used to make seasonal climate predictions whose skill is routinely evaluated (e.g., Kirtman et al., 2013²⁸, Merryfield et al., 2013³⁶; Sigmond et al., 2013⁴⁷; Kharin et al., 2017²⁷).

There are, however, uncertainties that have to be considered when using model projections. These uncertainties stem from the fact that models cannot simulate all physical processes exactly (and therefore must make approximations), and from internal variability in both the simulated and the real climate system (see Chapter 2, Box 2.5). The uncertainty due to approximations of physical processes can be reduced, in principle, and models continue to improve in this regard (Flato et al., 2013¹⁴). However, it is impossible to reduce the uncertainty from internal variability that is superimposed on the underlying forced climate change. In addition, there is uncertainty about what future climate forcing (e.g., future GHG emissions) will be, which is accounted for by making projections with a range of forcing scenarios. These sources of uncertainty vary in importance depending on the time and space scale under consideration — generally, uncertainties diminish at larger spatial scales as internal variability “averages out” to a certain degree when one considers larger regions (e.g., Hawkins and Sutton, 2009²¹). This also means that uncertainty is larger when one looks at small regions or specific locations. In addition, at longer time scales (say, by the end of the 21st century), uncertainty is dominated by differences in the forcing scenarios and internal variability is, by comparison, much smaller.

As described in Section 3.2, climate projections are a result of driving climate models with different future forcing scenarios (RCPs, in the case of CMIP5). These projections include the response of the climate system to external forcing (e.g., changing GHG concentrations), internal variability, and uncertainties associated with differences between models. These effects can be separated, to some extent, by drawing upon projections from multiple models (e.g., Collins et al., 2013⁵). The multi-model average provides an estimate of the response of the climate system to forcing, since internal variability and model differences are “averaged out” to a large extent (see Box 3.2). The upper panel of Figure 3.6 shows the change over time in global mean surface air temperature, as simulated by the CMIP5 models, spanning the period from 1950 to 2100. The heavy lines indicate the multi-model average, and the shaded band represents the range of model results around this average. Within this shaded band, each individual model result would look like one of the individual coloured lines in Figure 3.5, but for clarity this collection of individual lines is shown as a shaded band. The high emission scenario (RCP8.5) results are shown by the red line and the orange shaded band, whereas the low emission scenario (RCP2.6) results are shown by the blue line and the blue shaded band.

There are two key points illustrated in the upper panel of Figure 3.6. First, when looking at projected climate change, the spread across models (the vertical extent of the shaded bands) is smaller in the near term (to around 2040) than it is toward the end of the 21st century, indicating that model uncertainty has a larger effect further into the future. (Internal variability also contributes to the width of the shaded bands, as described previously, but the size of this contribution is not expected to change significantly in the future.) Second, the differences among forcing scenarios are small in the near term, but become large toward the end of the 21st century (as illustrated by the growing separation between results for the low emission scenario [RCP2.6] and high emission scenario [RCP8.5]). For simplicity, the medium emission scenarios (RCP4.5 and RCP6.0) are not shown in the main part of the figure, but their end-of-century results are shown on the right-hand side of the top panel for comparison.

The spatial patterns of projected temperature and precipitation change are shown in the bottom panel of Figure 3.6. The large difference in mean change between the high and low emission scenarios is clearly evident in the maps (darker colours indicate larger change), but there is a marked similarity in pattern. For temperature, changes are larger over land than over the adjacent ocean, and are larger at high latitudes, particularly over the Arctic, an illustration of Arctic amplification. As a result, projected warming in Canada is roughly double the global mean. For precipitation, the pattern of change is more complex, with the polar and equatorial regions projected to have increased annual precipitation, whereas precipitation decreases are projected for much of the subtropics (roughly 24° to 35° north and south latitude). For southern Canada, the projected change in precipitation is rather small, but projected increases are larger further north. (Changes in annual mean precipitation do not translate directly into changes in seasonal snow cover or water availability, as discussed in Chapter 5 and Chapter 6.)

The spatial patterns of projected temperature and precipitation change are shown in the bottom panel of Figure 3.6. The large difference in mean change between the high and low emission scenarios is clearly evident in the maps (darker colours indicate larger change), but there is a marked similarity in pattern. For temperature, changes are larger over land than over the adjacent ocean, and are larger at high latitudes, particularly over the Arctic, an illustration of Arctic amplification. As a result, projected warming in Canada is roughly double the global mean. For precipitation, the pattern of change is more complex, with the polar and equatorial regions projected to have increased annual precipitation, whereas precipitation decreases are projected for much of the subtropics (roughly 24° to 35° north and south latitude). For southern Canada, the projected change in precipitation is rather small, but projected increases are larger further north. (Changes in annual mean precipitation do not translate directly into changes in seasonal snow cover or water availability, as discussed in Chapter 5 and Chapter 6.)

On average, the models project a future global mean temperature change (relative to the 1986–2005 reference period) of about 1°C for the low emission scenario (RCP2.6) and 3.7°C for the high emission scenario (RCP 8.5) by the late 21st century, with a 5%–95% range of about 1°C above and below the multi-model average. This change is over and above the 0.6°C change that had already occurred from 1850 to the reference period. Therefore, the average projected change under the low emission scenario is consistent with the global temperature target in the Paris Agreement of limiting global warming to between 1.5°C and 2.0°C, although the projected range from all models extends both below and above this target. The low emission (RCP2.6) scenario requires emissions of CO₂ to peak almost immediately and reduce to near zero before the end of the century. Recent studies (e.g., Millar et al., 2017³⁷) provide more detailed analysis of scenarios that will limit warming to 1.5°C, and these also involve very rapid and deep emission reductions.

More details regarding future projections, with a focus on Canada, are provided in other chapters of this report. Confidence in climate change projections varies by region and by climate variable. So, for example, confidence in temperature change is higher than confidence in precipitation change. This is in large part because temperature change is a direct consequence of radiative forcing, whereas precipitation change is affected by a number of complex interactions, including changes in the water-holding capacity of a warming atmosphere, in global atmospheric circulation, in evaporation, and in other factors (e.g., Shepherd, 2014⁴⁶) (see Chapter 4). Changes in snow and ice are a consequence of changes in both temperature and precipitation and are discussed in more detail in Chapter 5. Freshwater availability (see Chapter 6) and ocean changes (see Chapter 7) are also affected by changes in temperature and precipitation, as well as by other factors.

Earth system models can be run in two different ways: one in which GHG concentrations are set and another in which GHG emissions are set (both are available as part of the RCP datasets). Concentration-driven simulations allow scientists to assess the difference, from one model to another, in how the climate responds to identical changes in GHG concentrations in the atmosphere. This helps separate the response of the climate system to a change in forcing (e.g., change in GHG concentrations) from the effect of carbon-cycle feedbacks involving the terrestrial and oceanic biospheres. The response of these natural carbon sinks to atmospheric CO₂ levels and to climate change will influence anthropogenic emissions compatible with a given CO₂ pathway. Therefore, an interesting aspect of these concentration-forced simulations is that global anthropogenic emissions can be computed — emissions that are compatible with the prescribed concentration pathway (e.g., Jones et al., 2013²⁵). The range in compatible CO₂ emissions between different models provides a measure of the uncertainty inherent in representing carbon-cycle feedbacks in models. Figure 3.7 illustrates results from compatible emission calculations and shows that, while there is some variation, this group of models is consistent. For the RCP 2.6 scenario in which temperature is stabilized below about 2°C, the models have compatible emissions that start reducing immediately and reach near zero well before the end of the century.

In summary, many Earth system models have been developed and used to make projections of future climate. Uncertainty in these projections arises from internal climate variability, from shortcomings in the models themselves, and from differences between plausible future forcing scenarios. Analysis of the entire collection of model results allows the first two sources of uncertainty to be reduced (though not eliminated), as model errors and internal variability are reduced by averaging across models. In the near term, to about 2040, the differences between forcing scenarios is not large. By the end of the 21st century, however, the global mean temperature increase projected for a low emission scenario is roughly 1°C, while for a high emission scenario it is roughly 4°C. The lower emission scenarios require rapid cuts in human emissions.

The IPCC Fifth Assessment Report found that warming induced by CO₂ at any point in time since the beginning of the Industrial Era is proportional to the total amount of CO₂ emitted up to that time (cumulative CO₂ emissions; IPCC, 2013²³). This relationship has been seen in a range of climate models, across a range of emissions pathways, and even at high levels of cumulative emissions (Tokarska et al., 2016⁵²). Figure 3.8 shows that average warming is closely proportional to cumulative CO₂ emissions for the CMIP5 models’ simulation of a CO₂ increase of 1% per year (thin black line). In this idealized simulation, atmospheric CO₂ concentration increases from its 1850 value of around 285 ppm by 1% per year until its concentration quadruples in 140 years to about 1140 ppm. The relationship between cumulative emissions of CO₂ and global mean surface temperature (GMST) is altered somewhat by the effects of other climate forcing agents (such as CH₄, N₂O, and various aerosols) that are included in the RCP scenarios, as shown by the divergence of the coloured lines in Figure 3.8 from the thin black CO₂-only line. Yet the total warming (due to CO₂ and other climate forcing agents) is approximately the same, as a function of cumulative emissions, across the four RCP scenarios shown in Figure 3.8. There is uncertainty in the relationship between warming and cumulative emissions, indicated by the shaded bands in the figure, and this must be taken into account when interpreting the results.

This relationship between cumulative CO₂ emissions and the increase in GMST can be used to estimate the maximum amount of CO₂ that can be emitted while limiting the temperature increase to a certain level. So, for example, in order to limit global warming to less than 2°C, as agreed in the Paris Agreement (UNFCCC, 2015⁵³), cumulative emissions of CO₂ must stay below a given level. Because of the uncertainty in this relationship, a likelihood must be attached to this level. Hence, the IPCC (2013) assessed that, to have a 50% chance of keeping global warming to less than 2°C, CO₂ emissions from 2011 onward would have to remain below 1300 billion tonnes of CO₂ (GtCO₂), roughly equal to what has already been emitted since the beginning of the Industrial Era. For a 50% chance of keeping the temperature increase to less than 1.5°C, emissions from 2011 onward would have to be limited to 550 GtCO₂. Similar carbon emissions budgets were obtained using an integrated assessment model driven by a broader range of scenarios, an approach that may be more robust (Rogelj et al., 2016⁴²). The median IPCC (2014) 1.5°C emissions budget of 550 GtCO₂ relative to 2011 is only 13.8 years of CO₂ emissions at current levels of approximately 40 Gt CO₂ per year, and we have already used about six years of this. However, several recent studies calculated this budget using an alternative approach, based on an estimate of human-caused global warming from pre-industrial times to 2015 of approximately 0.9°C (e.g., Millar et al., 2017³⁷). This leaves room for an additional approximately 0.6°C of warming to be consistent with a 1.5°C target. From this, cumulative carbon emissions budgets consistent with limiting warming to 0.6°C relative to 2010–2019 with 50% or more chance were estimated to be 760–850 GtCO₂ (Millar et al., 2017³⁷; Goodwin et al., 2018¹⁹; Tokarska and Gillett, 2018⁵¹), substantially more than the 390 GtCO₂ (from 2015) assessed by IPCC (2014). Conversely, accounting for carbon-cycle feedbacks involving permafrost, which were not included in the models assessed by IPCC (2014), would somewhat increase the warming for a given level of CO₂ emissions and hence somewhat reduce the emissions budgets, particularly at higher warming levels (MacDougall et al., 2015³¹). The upcoming IPCC Special Report on Global Warming of 1.5°C will comprehensively assess these emissions budgets and give an updated estimate of the remaining allowable emissions to meet the global temperature target under the Paris Agreement.

Earth system model simulations of the response to CO₂ emissions show that GMST remains approximately constant for many centuries following a cessation of emissions (Collins et al., 2013⁵). For example, GMST remains high in two simulations of Environment and Climate Change Canada’s first-generation Earth system model, CanESM1, under a scenario in which CO₂ emissions increase and subsequently cease, being reduced to zero in 2010 or in 2100 (Figure 3.9; Gillett et al., 2011¹⁸). Similar results are obtained using other models (e.g., Matsuno et al., 2012³⁴; Matthews and Caldeira, 2008³⁵; Frölicher and Joos, 2010¹⁶). Thus, regardless of when emissions cease, GMST remains approximately constant for the subsequent millennium.

Ceasing emissions of aerosols, which are short-lived and that largely exert climate-cooling effects (see Box 3.3) would lead to rapid warming, whereas ceasing short-lived GHG emissions would cause cooling (Collins et al., 2013⁵). The response to a cessation of emissions of other long-lived GHGs is qualitatively similar to that to CO₂ (Smith et al., 2012⁴⁸), taking a very long time to reduce temperature. While GMST is expected to remain constant after emissions cease, other aspects of the climate system are expected to continue to change. Vegetation, ice sheet volume, deep ocean temperature, ocean acidity, and sea level are projected to change for centuries after stabilization of GMST (Collins et al., 2013⁵).

In summary, many aspects of climate change are irreversible on multi-century timescales. CO₂ persisting for a century or more in the atmosphere is the main determinant of global mean temperature change, and global temperature will remain elevated even after emissions cease. GMST could be reduced only if human intervention could remove CO₂ from the atmosphere over a sustained period.

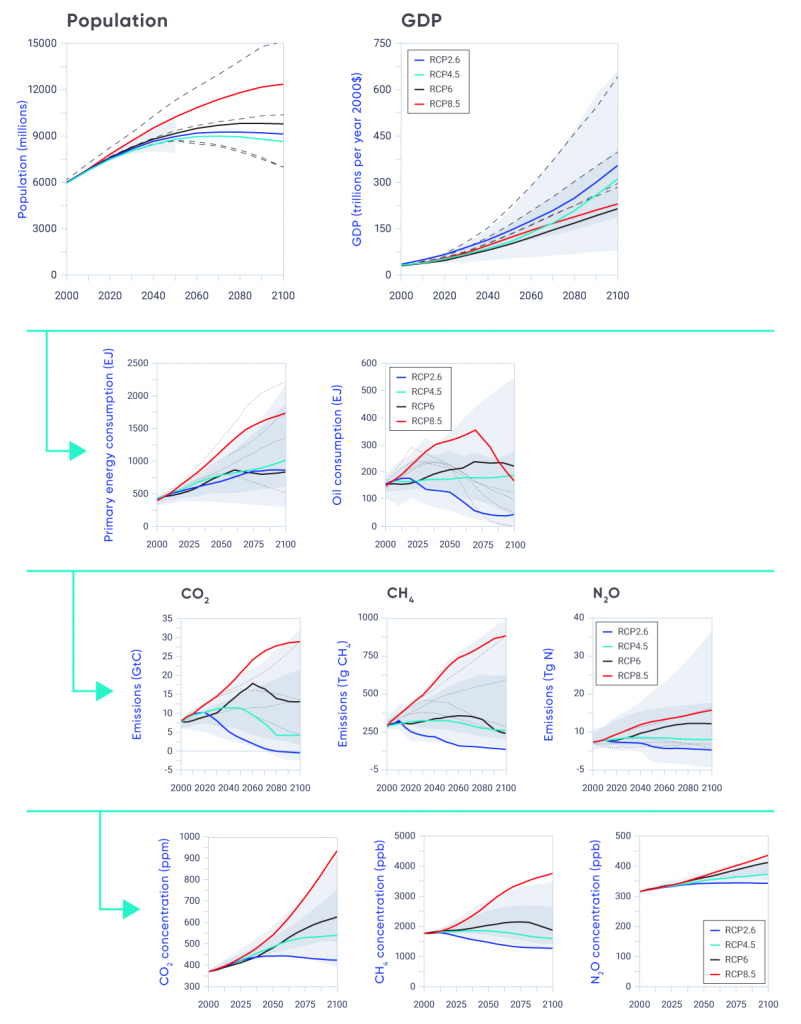
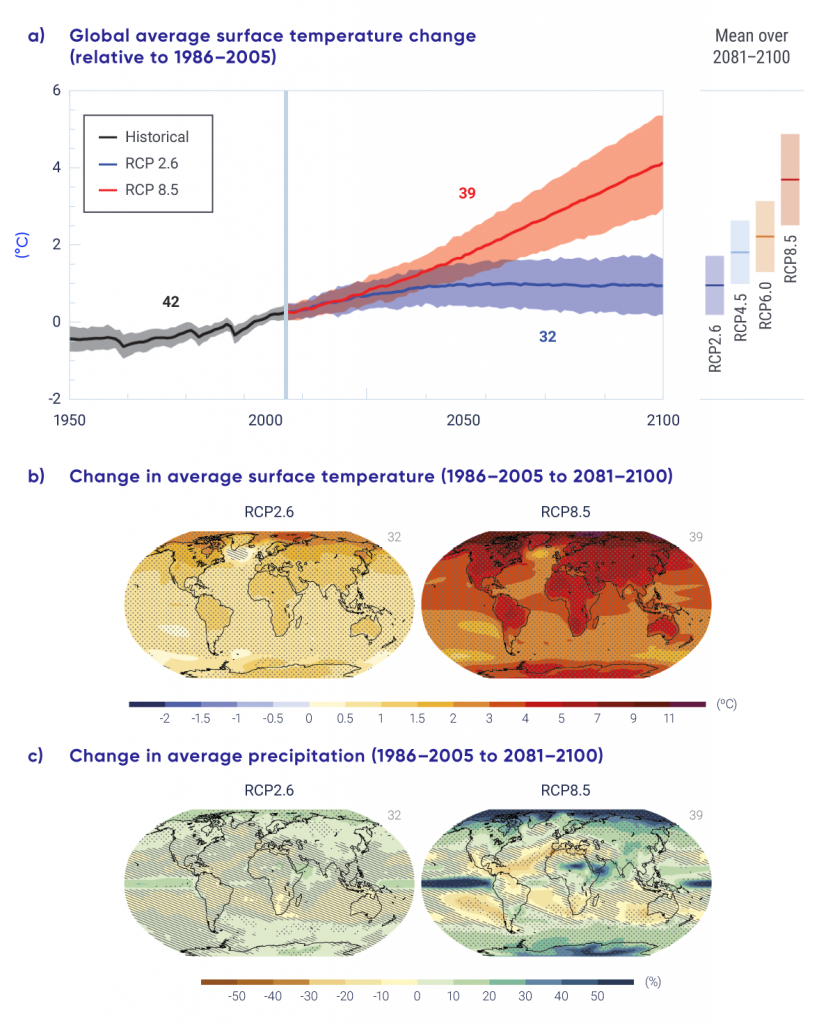
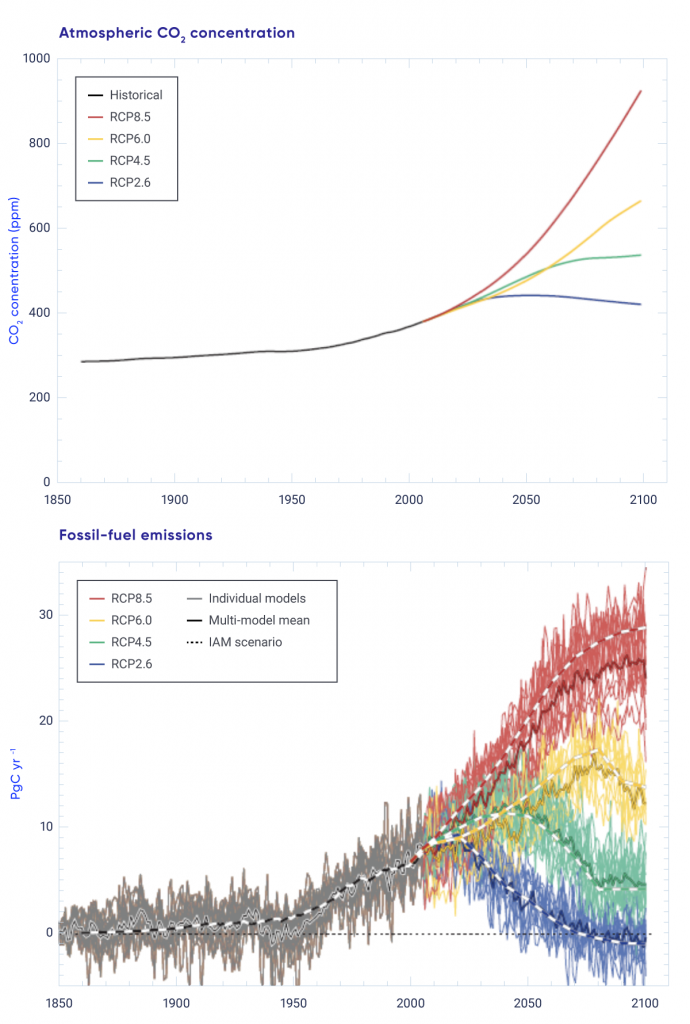
Climate projections must be made using global models because many of the processes and feedbacks that shape the response of the climate system to external forcing operate at the global scale. For many applications, where only the change in some climate quantity is needed, global model projections can be used directly. This is because climate change normally applies over a much larger area than the climate itself, which can vary markedly over short distances in some regions. This is particularly the case for projected change in temperature, which has a very broad spatial structure, although local temperature may differ between, for example, the bottom of a valley and the surrounding hillsides.

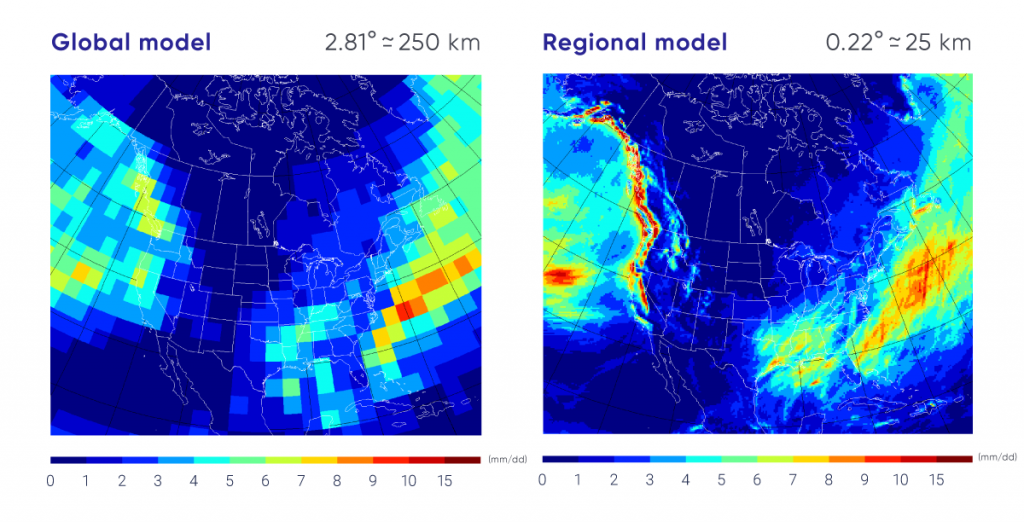
However, for other applications, global climate model projections are not adequate, as they typically have horizontal spatial resolution, or grid spacing, of 100 km or coarser (see Figure 3.2 for explanation of model characteristics) (e.g., Charon, 2014³). As an example, when using climate projections to drive a detailed hydrological model at the scale of a drainage basin, one needs values of future climate variables at a scale that respects local topographic, coastal, and other features, and represents high-frequency variability and extremes. Users of climate projections must therefore first evaluate whether they really need high-resolution climate scenarios or whether they could make effective use of lower-resolution climate change scenarios. Higher resolution, in and of itself, does not necessarily indicate higher-quality or more valuable climate information. But, for many applications, higher resolution may be necessary, and can also facilitate better understanding among, and communication to, users. A caution, however, is that internal climate variability is reduced by averaging results over large areas, and so as one goes from global to regional to local scale, internal variability becomes larger, leading to larger uncertainty in projections at the local scale, relative to that at regional or global scale (Hawkins and Sutton, 2009 ²¹).

When climate information at a higher spatial- or temporal-resolution is needed, there are several approaches available to take global climate model projections and “downscale” them to higher resolution for a region of interest (or even a single location). These generally fall into two categories: statistical and dynamical downscaling.

Statistical downscaling is a form of climate model “post-processing” that combines climate model projections with local or regional observations to provide climate information with more spatial detail (Maraun et al., 2010³³; Hewitson et al., 2014²²). Statistical post-processing methods typically downscale to higher resolution and correct systematic model biases. A simple example is the so-called “delta method,” in which the change in some climate quantity, obtained from a climate model projection, is added to the observed historical value of that quantity. This allows projected changes from different climate models to be used in a consistent manner, since each model’s climatological bias is eliminated. Bias correction is particularly important when using downscaled climate information to drive impact models that depend on crossing absolute thresholds. For example, snow accumulation is sensitive to whether temperature is above or below freezing.

Simple techniques like the delta method may be suitable for some quantities, such as mean temperature, but not for others, such as daily precipitation, for which biases may be manifested differently, in variability, extremes, or dry/wet spells (Maraun et al., 2010³³). More complex statistical downscaling approaches are required in such cases, making use of detailed high-resolution observational datasets that reflect local topographic influences. These high-resolution data are used to interpolate low-resolution climate change projections to much higher resolution. In some cases, bias correction and other refinements are applied to correct statistical properties such as variances (Werner and Cannon, 2016⁵⁶). Yet other statistical downscaling methods take advantage of observed relationships between large-scale atmospheric circulation patterns, which are often well simulated by climate models, and local variables. By assuming that these statistical relationships remain fixed under a changing climate, climate model projections of circulation patterns can be used to make projections of future climate at a particular location. The statistical relationships introduce some aspects of local climate that may not be well represented in the driving global model (e.g., local topography and proximity to a lake). Fundamentally, all statistical downscaling methods assume that relationships between a model’s historical simulation and observations do not change over time, and that the information provided by the climate model and historical observations at their respective spatial scales is credible. Thus, the quality of statistical downscaling is directly related to the quality and availability of observational data. Recent critical reviews provide more information on the strengths and weaknesses of statistical downscaling and bias correction methods (Hewitson et al., 2014²²; Maraun, 2016³²).

Dynamical downscaling involves the use of a regional climate model, which is a physically based climate model (of the same level of complexity as a global model) that operates at high resolution over a limited area. Regional climate models incorporate much the same physical processes and scientific understanding as global climate models and indeed often share much of the same computer code. The important distinction is that regional climate models are driven at their lateral boundaries by output from a global climate model, as shown in Figure 3.10. The regional model also inherits errors and biases that may be present in the global model whose results are provided at the boundaries. The main advantage of dynamical downscaling is that, due to its limited area, a regional model can simulate climate on a much higher resolution than is possible with a global model, using a similar amount of computing effort. This additional detail is often desirable, particularly where the regional model output is used to drive another model (e.g., a hydrological model in which detailed basin geometry, high-frequency precipitation and extremes, and other small-scale features are essential). However, it remains an ongoing research topic to determine whether, and under what conditions, regional models add value relative to the original global model results that are being downscaled. There are no agreed-upon measures for added value (Di Luca et al., 2015¹⁰; 2016⁸; Scinocca et al., 2016⁴⁵), although the evidence available at the time of the IPCC Fifth Assessment indicated that there is added value in some locations owing to the better representation of topography, land/water boundaries, and certain physical processes, and that extremes are better simulated in high-resolution regional models (e.g., Flato et al., 2013¹⁴).

An additional advantage of dynamical over statistical downscaling is that physical relationships between different climate variables (such as temperature and precipitation) are maintained. For very-high-resolution dynamical downscaling (at model resolution of a few kilometres), physical processes such as convection can be resolved explicitly and can lead to improved simulation of climate variables such as precipitation extremes. Several recent studies indicate added value, including a dynamical downscaling system that includes a detailed representation of the Great Lakes (Gula and Peltier, 2012²⁰), the potential for added value near well-resolved coastlines (Di Luca et al., 2013⁹), and evidence for improved simulation of temperature and precipitation extremes (Curry et al., 2016a⁶,b⁷; Erler and Peltier, 2016¹¹).

Both statistical and dynamical downscaling approaches have been applied and evaluated in many areas of the world. For North America, coordinated dynamical downscaling comparisons have been undertaken as part of the North American Regional Climate Change Assessment Program (NARCCAP: http://www.narccap.ucar.edu/) and the Coordinated Regional Downscaling Experiment (CORDEX: https://na-cordex.org/). For CORDEX, simulations were run at resolutions of approximately 25 km and 50 km. In both NARCCAP and CORDEX, Canadian models are represented. Coordinated experiments like these provide results from different regional climate models, driven at their boundaries by output from different global climate models. They also allow scientists to determine whether regional differences in projected climate change are related to the differences in the global driving models or to differences in the regional downscaling models. However, the CORDEX ensemble is considerably smaller than the CMIP global model ensemble, and studies using the CORDEX ensemble tends to focus on sub-regions rather than on Canada as a whole.

For Canada, regional climate models with smaller domains and higher resolution are being used, particularly by the Ouranos consortium and the Centre pour l’étude et la simulation du climat à l’échelle régionale (ESCER) at the Université du Québec à Montréal. Some of these simulations provide results at 15 km resolution (e.g., https://www.ouranos.ca/en/program/climate-simulation-and-analysis/). Statistical downscaling results are also readily available for Canada (https://www.pacificclimate.org/data/statistically-downscaled-climate-scenarios), with daily temperature and precipitation data at approximately 10 km resolution. These state-of-the-art downscaling approaches (Werner and Cannon, 2016⁵⁶) are driven by multiple global climate model projections. In addition to the more detailed spatial structure, sophisticated statistical downscaling approaches can also provide estimates of future changes in climate extremes and other indices (such as frequency of hot days, growing season length, and drought indices) that are particularly important for certain impact studies (see Chapter 4). Downscaled results can also be used as inputs to impacts models — such as hydrological, crop, and ecosystem models — that are sensitive to variability on small spatial scales and to biases in climate models (Wood et al., 2004⁵⁷).

In summary, global Earth system models are necessarily limited in the level of fine spatial detail they can resolve. Techniques such as statistical or dynamical downscaling allow transformation of these large-scale projections to a level of detail better suited to the climate information needs of many local and regional impact studies. It must be noted, however, that uncertainty due to internal climate variability is reduced by area averaging (e.g., averaging over Canada or the globe), and so uncertainty in climate projections is larger as one goes from global to regional to local scale.